Math help please - size and distance

[veryzebra]

If there is something I want to take a picture of, that is about 400' tall, and I want to be more than 400' away from it, How much of the frame would that fill up? Thanks

 

[veryzebra]

BTW, this is for the Mavic 3. Figured that was given since I posted in the Mavic 3 forum, but just in case : ) and using the base camera without zooming in. I've heard others say like a human at x yards away would fill up y% of the frame for a specific camera/lens combo. I'm looking for the math to gauge my distance based on what % of the frame the object is taking up. Thank you

 

[GadgetGuy]

If there is something I want to take a picture of, that is about 400' tall, and I want to be more than 400' away from it, How much of the frame would that fill up? Thanks

At what elevation will the drone be?

 

[Zbip57]

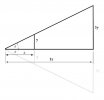
You could do a test to figure out what the field of view angle is. Place your Mavic on the ground, or on the edge of a table. Use an object that you know the precise height of, like a yardstick (y). Move the yardstick closer or further from your Mavic until it just fills the camera view from top to bottom. Now measure the distance from the camera lens to the yardstick (x).

The exact numbers don't matter. You just need to know the ratio between the two.

Let's say the item you're measuring is 4' tall (y), and needs to be 8' away from the lens (x) to fill the camera view top to bottom.

y/x = 4'/8' = 0.5

Once you know the scaling factor, you can apply that to any distance, scaled up or down. i.e. Something 10' tall would need to be 20' away to fill the frame.

I don't know what the actual number is, but if the scaling factor is 0.5 as in this example, a 400' tower would fill the frame if the Mavic was 800' away from it.

 

[HoozierDroneDaddy]

Keep in mind, you could also shoot two or three photos vertical or landscape and merge them.

 

[Lets Fly]

Or back off and crop it.

 

[veryzebra]

You could do a test to figure out what the field of view angle is. Place your Mavic on the ground, or on the edge of a table. Use an object that you know the precise height of, like a yardstick (y). Move the yardstick closer or further from your Mavic until it just fills the camera view from top to bottom. Now measure the distance from the camera lens to the yardstick (x).

The exact numbers don't matter. You just need to know the ratio between the two.

Let's say the item you're measuring is 4' tall (y), and needs to be 8' away from the lens (x) to fill the camera view top to bottom.

y/x = 4'/8' = 0.5

Once you know the scaling factor, you can apply that to any distance, scaled up or down. i.e. Something 10' tall would need to be 20' away to fill the frame.

I don't know what the actual number is, but if the scaling factor is 0.5 as in this example, a 400' tower would fill the frame if the Mavic was 800' away from it.

View attachment 151972

My geometry teacher in hs was hot so there wasn't a lot that I learned lol. But ah this, makes sense thanks.

 

[Zbip57]

My geometry teacher in hs was hot so there wasn't a lot that I learned lol. But ah this, makes sense thanks.

I actually learned this trick from a tree guy.

I needed to cut down a dead tree but wondered if the tree was tall enough and/or standing too close to hit our house when it came down. How do I measure the height of the tree?

I was thinking I'd need a long tape measure and a surveying transit to measure the angle to the top of the tree, then do some complicated trigonometry to calculate the height. But it turns out no math is required.

He said you just take something like a rake handle, a straight stick, an axe handle, whatever is handy, and grab it at a length so it's the same length as your outstretched arm (then x=y in my diagram above),

Hold that length of rake handle straight up at the end of your outstretched arm and walk away or toward the tree until the rake handle is superimposed top to bottom with the tree.

It doesn't matter if the tree is ten times or 400 times as tall as that axe handle is long. All that matters (as long as x equals y), now your standing right where the tip of the tree will land, because the distance to the base of tree (x) equals the height of the tree (y), where x and y are both equally scaled up ten times or 400 times, whatever...

Cool, huh?

 

[Zbip57]

I actually learned this trick from a tree guy.

There are lots of YouTube videos showing how this is done.

To view this content we will need your consent to set third party cookies.
For more detailed information, see our cookies page.

Accept third party cookies

 

[veryzebra]

I actually learned this trick from a tree guy.

I needed to cut down a dead tree but wondered if the tree was tall enough and/or standing too close to hit our house when it came down. How do I measure the height of the tree?

I was thinking I'd need a long tape measure and a surveying transit to measure the angle to the top of the tree, then do some complicated trigonometry to calculate the height. But it turns out no math is required.

He said you just take something like a rake handle, a straight stick, an axe handle, whatever is handy, and grab it at a length so it's the same length as your outstretched arm (then x=y in my diagram above),

Hold that length of rake handle straight up at the end of your outstretched arm and walk away or toward the tree until the rake handle is superimposed top to bottom with the tree.

It doesn't matter if the tree is ten times or 400 times as tall as that axe handle is long. All that matters (as long as x equals y), now your standing right where the tip of the tree will land, because the distance to the base of tree (x) equals the height of the tree (y), where x and y are both equally scaled up ten times or 400 times, whatever...

Cool, huh?

I still miss my math teacher lol

 

[GadgetGuy]

I still miss my math teacher lol

You still haven't told us at what elevation you intend to take the photos from.
It makes a huge difference in the answer!
Everyone else is assuming you are only shooting from the ground, in which case you certainly don't need the Mavic 3.

 

[veryzebra]

I'll be just under 100', thanks

 

[GadgetGuy]

I'll be just under 100', thanks

At 100’ of elevation, you will be able to fill the frame from a much closer distance than while on the ground. In the diagram in post #4, the field of view also extends below the base of the triangle when at 100', so the calculations need to be adjusted accordingly. The FOV of the main camera is 84°.

 

[Zbip57]

You still haven't told us at what elevation you intend to take the photos from.
It makes a huge difference in the answer!

Not really.

At 100’ of elevation, you will be able to fill the frame from a much closer distance than while on the ground. In the diagram in post #4, the field of view also extends below the base of the triangle when at 100', so the calculations need to be adjusted accordingly.

Actually, the elevation alone makes no difference at all. But the viewing angle of the gimbal does make a difference to how tall the tower appears in the camera view.

For example, looking square at it with the camera aimed horizontally you'll see the full height. But if you have the gimbal aimed straight down viewing the tower from directly above, then you'll only see the top of the tower.

But, I know what you mean. If you're shooting from ground level, you'd need to pitch the gimbal upwards to fill the camera frame with the tower. Otherwise, if shooting horizontally, the lower half of the screen would just be showing ground.

Similarly, if you're hovering at a height equal to the top of the tower, you'd need to angle the camera down to fill the frame with the tower, otherwise half of the view would only be sky.

If you fly at half the height of the tower, with the gimbal aimed horizontally, then you just need to fly closer or further away to fill the frame.

But none of that actually makes any difference to the method described in post#4 above. You just need to decide beforehand on what gimbal angle you're planning on using. Set the gimbal to that angle, then use the yardstick method as described.

The viewing angle affects the scale factor. Once you know the scale factor for the chosen viewing angle, all the rest remains the same. Twice as far away, the tower appears half the size.

 

[Zbip57]

The FOV of the main camera is 84°.

That's useful.

If you already know the field-of-view angle, then you can pre-calculate the scaling factor for any desired gimbal angle.

The green triangle is what it would look like with the gimbal aimed horizontally and the camera at ground level. You know the 400' vertical height of the tower, i.e. the vertical red line (y) showing above the horizon. To fill only the top half of your camera view (42°), you'd need to locate the camera at a distance of (x) away from tower.

x = y / tan(42°)
x = 400' / 0.9
x = 444.4'

But if you're not at ground level, but rather flying at half the height of the tower, still with the gimbal aimed horizontally, you can use the full 84° frame height, with 200' of the tower in the top half, and the other 200' in the bottom half of the screen. Here y=200'.

In that case x = 222.2'

So it appears as though elevation does make a difference. You're now shooting from half the distance, yes.

But realistically you would never have chosen to have the gimbal aimed horizontally when shooting from ground level. You would have aimed the camera up to fill the entire frame with the tower alone, rather than leaving the lower half of the camera view showing only the ground.

I'll illustrate what difference a non-horizontal view makes in the next post. Either way, the yardstick method of post#4 still works. You just need to know the scaling factor (y/x) for the chosen gimbal viewing angle. You can still use the simple yardstick measurement to approximate the scaling factor, or you can use math to calculate it if you already know the camera's field-of-view angle (here 84°). After that, twice the viewing height (y) requires twice the distance (x) to fill the camera view etc.

 

[MS Coast]

[EDIT: I think I was distracted by thinking about a high school teacher, too. She was a former mermaid at Weeki Wachi Springs in Florida. Anyway, the vertical FOV number here is not right. It's not related to the horizontal by the aspect ratio. See post #22. And I'd misunderstood the OP's question to be that he wanted to know at what distance would the building fill the frame vertically. So, it's best to just IGNORE THIS and move on.]

About 204 feet. If ...

The M3 main camera specs list a field of view of 84 degrees. If that's the horizontal field of view and the frame has a 4:3 ration, the vertical field of view is 63 degrees. [NOT]

The tangent of an angle is opposite side / adjacent side. The tangent of 63 degrees is 1.9626. So to completely fill the frame vertically, you'd want the ratio of the building height to the setback distance to be 1.9626. That makes the setback distance 204' if you're at the same level as either the top of bottom of the building.

In between those heights, there will be a small difference. Not worth worrying about, since you're probably going to want to tinker with the view a bit rather than having the building exactly fill the frame.

Caveats:
Not accurate if the 84 degree FOV figure in the M3 specs is the diagonal FOV rather than the horizontal FOV. Anyone know for sure?

Edit: I see that @Zbip57 just posted something similar, but with the assumption that the 84 degree FOV is the vertical FOV. I suspect it's actually the horizontal FOV.

 

[Zbip57]

Edit: I see that @Zbip57 just posted something similar, but with the assumption that the 84 degree FOV is the vertical FOV. I suspect it's actually the horizontal FOV.

D'oh! Of course that would make a difference.

But, that just further illustrates that it's difficult to calculate this stuff with trigonometry, when it's so much simpler to just use the yardstick method as a fairly close approximation.

 

[Zbip57]

This one gets a bit more complicated, but bear with me. When shooting at an angle the scaling factor changes. But the yardstick method still works exactly the same. You just need to decide beforehand on what angle the gimbal will be aimed at.

In this example we're shooting with the gimbal aimed 30° below horizontal. Assuming the camera still has an 84° vertical field-of-view angle, one can do the following calculations (or adjust them once the proper number is known ).

With the gimbal aimed down 30°, that leaves 12° of the view above horizontal and 72° below horizontal (total 84°). And we know the portion of the tower above horizontal (y above), plus the portion below horizontal (y below) totals 400' in vertical length. Solve for x.

ya + yb = 400'

tanθ = y/x
x (tan(12°)) = ya
x (tan(72°)) = yb

x = 400' / (tan(12°)+tan(72°))
x = 400' / (0.2126 + 3.077)
x = 400 / 3.2896
x = 121.6'

 

[Zbip57]

Ouch. That's far too complicated. And it's all based on the questionable assumption that the camera's vertical field-of-view is 84°.

The yardstick method really is much simpler. Note that in both illustrations an item twice as tall must still be placed twice as far away to fill the total field-of-view.

So, if you plan to shoot with your gimbal aimed 30° down from horizontal, set it now to that angle (or any other desired angle).

Place your drone at the edge of a table and hold a vertical yardstick, or any other item of known length (y), in front of the drone so that the yardstick fills the camera view top to bottom. Now measure the horizontal distance (x) between the camera lens and your yardstick.

Presto, you've got your scaling factor (y/x). If you want to fill your screen with an object that's 50 times taller than your yardstick, you need to horizontally move your camera back to a distance of 50 times x.

Conversely, you could even use this yardstick method to approximate the actual field-of-view angle of your camera.

It's simpler if the gimbal is aimed horizontally. With the length of your yardstick filling the camera view top-to-bottom, half above the horizontal and half below, then;
y = half the length of the yardstick
x = distance between yardstick and camera.
θ = field-of-view angle (nope, see correction edit below)

tan(θ) = y/x
θ = arctan(y/x)

-----
edit: Ack! On second thought, the formula (for a 90° right-angled triangle) calculates only the top half of the field-of-view angle. That's only the green portion of the triangle shown in post#15 above. In this example, the total field-of-view angle would, of course, be twice the calculated θ angle.

 

[MS Coast]

I just re-read the OP's post and better understood what he's asking. He wants to be at least 400' from the 400' tall object and want's to know how much of the screen would be filled vertically.

400' out from a 400' object means the angle to the top from ground level is 45 degrees. (Tan (45) - 1) If the vertical field of view of the main camera is 63 degrees the object will fill 45/63 of the frame. So just a bit more than 70%.