The Terminal Velocity of a Falling Mavic 2

[Drbobk]

First second it travels 16' but in that one second it has accelerated to 32 FPS. (Starts at 0 FPS, accelerates to 32FPS, and thus averages 16FPS for the first second.) It travels 48' in the second second, and accelerates from 32FPS to 64FPS, and so on.

 

[mikemoose55]

First second it travels 16' but in that one second it has accelerated to 32 FPS. (Starts at 0 FPS, accelerates to 32FPS, and thus averages 16FPS for the first second.) It travels 48' in the second second, and accelerates from 32FPS to 64FPS, and so on.

Until a falling object reaches "terminal velocity" which is when the wind resistance against the object in free fall becomes great enough to cancel any further acceleration from gravity.

You see this when you drop a hammer and a feather. The hammer hits first even though the acceleration rate is exactly the same for both the hammer and the feather. The difference being the feather reaches treminal velocity almost instantly so acceleration rate stops while the hammer will continue to pick up speed for quite a long while.

In the absence of atmosphere the hammer and the feather will accelerate equally and hit at exactly the same time.
here is the famous test from the surface of the moon showing the feather and hammer falling and landing exactly the same time.

mikemoose55

 

[AMann]

My 7th graders used two identical plastic balls, filled one up with water, the other just air. Dropped from a third story level and they identically hit the ground. Air resistance was the same for both spheres, mass was not.

 

[mikemoose55]

My 7th graders used two identical plastic balls, filled one up with water, the other just air. Dropped from a third story level and they identically hit the ground. Air resistance was the same for both spheres, mass was not.

Do you think the result would have been the same if you dropped both again but this time from 33rd floor?

 

[AMann]

Do you think the result would have been the same if you dropped both again but this time from 33rd floor?

Yup- but the 13th floor may have been different ... and the 30th floor would have been chaos.

 

[FoxhallGH]

Until a falling object reaches "terminal velocity" which is when the wind resistance against the object in free fall becomes great enough to cancel any further acceleration from gravity.

You see this when you drop a hammer and a feather. The hammer hits first even though the acceleration rate is exactly the same for both the hammer and the feather. The difference being the feather reaches treminal velocity almost instantly so acceleration rate stops while the hammer will continue to pick up speed for quite a long while.

In the absence of atmosphere the hammer and the feather will accelerate equally and hit at exactly the same time.
here is the famous test from the surface of the moon showing the feather and hammer falling and landing exactly the same time.

mikemoose55

Next we'll have explanations of how that video was faked by the conspiracy theorists who don't believe that man ever walked on the Moon ..
That's a great video ...

 

[sar104]

Until a falling object reaches "terminal velocity" which is when the wind resistance against the object in free fall becomes great enough to cancel any further acceleration from gravity.

You see this when you drop a hammer and a feather. The hammer hits first even though the acceleration rate is exactly the same for both the hammer and the feather. The difference being the feather reaches treminal velocity almost instantly so acceleration rate stops while the hammer will continue to pick up speed for quite a long while.

In the absence of atmosphere the hammer and the feather will accelerate equally and hit at exactly the same time.
here is the famous test from the surface of the moon showing the feather and hammer falling and landing exactly the same time.

mikemoose55

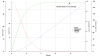
If we are going to get that far into the details then this needs some clarification. Objects don't accelerate at 9.8 m/s² until they reach terminal velocity, and then discontinuously stop accelerating. The rate of acceleration follows from Newton's 2nd Law (F = ma), where F is the weight of the object minus the aerodynamic drag, which is approximately proportional to the square of the air speed v. So,

a = (mg - kv²)/m = g - kv²/m​

where k is the constant of proportionality in the form:

k = ρcA/2​

where ρ is the air density, A is the effective cross-sectional area and c is a geometric factor, which is approximately unity for a flat(ish) shape. So while the instantaneous initial acceleration of any object is g, it immediately starts to decrease for all v > 0.

If we take the cross-sectional area of a Mavic 2 to be about 25 cm x 25 cm (a conservative estimate including the propellers) and its mass to be 0.9 kg, and the and solve the resulting differential equation, we get the following acceleration, speed and distance as a function of time, which is actually quite consistent with observed falling Mavics.

 

[Drbobk]

I hate it when I get out-geeked. Well done!

 

[Drbobk]

I imagine that the props might create an autorotation effect on the falling Mavic, and might even keep it upright if it fell from high enough. I think that might be even more likely with my Inspire based on its shape and weight distribution. Has anybody seen such an effect with a falling drone?

 

[AMann]

I imagine that the props might create an autorotation effect on the falling Mavic, and might even keep it upright if it fell from high enough. I think that might be even more likely with my Inspire based on its shape and weight distribution. Has anybody seen such an effect with a falling drone?

Nice, you’ve got Sar104 erasing his entire chalkboard!

 

[sar104]

I imagine that the props might create an autorotation effect on the falling Mavic, and might even keep it upright if it fell from high enough. I think that might be even more likely with my Inspire based on its shape and weight distribution. Has anybody seen such an effect with a falling drone?

The calculation above is actually based on some amount of prop rotation and stabilization in the choice of cross-sectional area and drag form factor. There are not much data to go on as far as falling with all motors off - I haven't been able to get hold of a DAT file for a mid-air CSC. Most falling drones are falling because they lost a prop or motor, and they do tumble and rotate as the FC attempts to stabilize with 3 motors. What's interesting, however, is that the terminal velocities achieved tend all to be similar, probably because of the v² dependence of the drag force.

 

[AMann]

The calculation above is actually based on some amount of prop rotation and stabilization in the choice of cross-sectional area and drag form factor. There are not much data to go on as far as falling with all motors off - I haven't been able to get hold of a DAT file for a mid-air CSC. Most falling drones are falling because they lost a prop or motor, and they do tumble and rotate as the FC attempts to stabilize with 3 motors. What's interesting, however, is that the terminal velocities achieved tend all to be similar, probably because of the v² dependence of the drag force.

Your analysis is very interesting to follow. It does seem that they really don’t stabilize at all during freefall - so I’ve wondered how dependable those fall recovery systems really are as the parachute would tend get entangled if the drone is tumbling.

 

[sar104]

Just for comparison, if you were to remove the props, fold back the arms and fin-stabilize the Mavic so that it went into a straight dive in the lowest possible drag configuration, you get the following profile:



Quite a difference.

 

[Mav1c]

Just for comparison, if you were to remove the props, fold back the arms and fin-stabilize the Mavic so that it went into a straight dive in the lowest possible drag configuration, you get the following profile:

View attachment 65610

Quite a difference.

156mph vs 40moh?!? Wow.

Just curious.. how did you get these graphs?

 

[sar104]

156mph vs 40moh?!? Wow.

Just curious.. how did you get these graphs?

That's explained in post #27. They show the solutions to the differential equations that describe drag-limited motion in a fluid applied to a nominal Mavic-like object in the atmosphere.

If you mean how, specifically, did I create them - I used the data analysis package Igor Pro to solve the differential equations numerically and plot the results.

 

[Mav1c]

That's explained in post #27. They show the solutions to the differential equations that describe drag-limited motion in a fluid applied to a nominal Mavic-like object in the atmosphere.

If you mean how, specifically, did I create them - I used the data analysis package Igor Pro to solve the differential equations numerically and plot the results.

Ahhh I see. These are all of your calculations with data you inputted from various sources. I wasn’t sure if it was some sort of dji software taken from flight data. I’ve seen a lot of your flight analysis and I’m always intrigued and impressed. Great work!!

I find myself just as interested in drone incidents/crash investigations as I am with manned aviation. I’ve read countless of NTSB reports and I find them both fascinating and poignant at the same time..

 

[sar104]

Ahhh I see. These are all of your calculations with data you inputted from various sources. I wasn’t sure if it was some sort of dji software taken from flight data. I’ve seen a lot of your flight analysis and I’m always intrigued and impressed. Great work!!

I find myself just as interested in drone incidents/crash investigations as I am with manned aviation. I’ve read countless of NTSB reports and I find them both fascinating and poignant at the same time..

Yes - those are basic physics calculations based on simple fluid dynamics, standard drag coefficient ratios, and the shape of a Mavic. They could be further refined with actual experimental data but there are not enough available flight logs for free-falling drones. For some reason people seem reluctant to experiment.

 

[zxcflyer]

The calculation above is actually based on some amount of prop rotation and stabilization in the choice of cross-sectional area and drag form factor. There are not much data to go on as far as falling with all motors off - I haven't been able to get hold of a DAT file for a mid-air CSC. Most falling drones are falling because they lost a prop or motor, and they do tumble and rotate as the FC attempts to stabilize with 3 motors. What's interesting, however, is that the terminal velocities achieved tend all to be similar, probably because of the v² dependence of the drag force.

Here is a DAT file with three mid-air CSCs. What can you tell us from these? Ignore the part after 400 seconds.

 

[sar104]

Here is a DAT file with three mid-air CSCs. What can you tell us from these? Ignore the part after 400 seconds.

Excellent. And three of them? I know what I'm doing this evening. Stand by.

 

[sar104]

Very interesting. The three power-off events show similar initial evolution of pitch, roll and yaw, followed by varied, possibly chaotic, behavior:






The vertical speed reflects that, with a transition to oscillatory behavior as the aircraft wobbles:







The blue dotted lines are the model that I posted previously, with a slightly lower drag coefficient than my initial guess (0.025 rather than 0.031), and predict the motion pretty well. The terminal velocity of around 20 m/s (45 mph) is in line with previous data and reports.